REMEDIAL PTS
Akan dibuktikan untuk n = 1 Benar
(2n – 1) = n²
2(1) – 1 = 1²
2 – 1 = 1
1 = 1 (benar)
Langkah kedua
Misal untuk n = k benar
1 + 3 + 5 + 7 + ... + (2k – 1) = k²
Akan dibuktikan untuk n = (k + 1) juga benar
1 + 3 + 5 + 7 + .... + (2k – 1) + (2(k + 1) – 1) = (k + 1)²
|__________________|
k² + (2(k + 1) – 1) = (k + 1)²
k² + 2k + 2 – 1 = (k + 1)²
k² + 2k + 1 = (k + 1)²
(k + 1)² = (k + 1)²
(Benar)
Jadi TERBUKTI bahwa 1 + 3 + 5 + 7 + ... + (2n – 1) = n² berlaku untuk setiap n bilangan asli.
3. Pembuktian Rumus Deret Geometri
Deret geometri adalah jumlah n suku pertama dari barisan geometri. Barisan geometri adalah barisan yang memiliki rasio tetap atau memiliki pengali yang tetap antar suku yang berurutan. Secara umum suku ke-n barisan geometri yang memiliki suku pertama a dan rasio r adalah sebagai berikut.
Un=arn-1
Barisan geometri untuk n suku pertama dapat dituliskan sebagai berikut.
U1, U2, U3, U4, ... , Un
a, ar, ar2, ... , arn-1
Jumlah n suku pertama barisan geometri di atas disebut sebagai deret geometri. Misal jumlah n suku pertama barisan geometri di atas adalah Sn maka Sn dapat dituliskan sebagai berikut.
Sn = a + ar + ar2 + ... + arn-1
Sn = a(1 + r + r2 + ... + rn-1)
Untuk memperoleh rumus umum dari deret geometri di atas, kita perlu membuat persamaan lain sehingga bentuk di atas menjadi lebih sederhana. Caranya adalah dengan mengalikan Sn dengan r, sehingga setiap suku dari penjumlahan n suku pertama barisan geometri di atas dikalikan juga dengan rasio (r).
rSn = ar(1 + r + r2 + ... + rn-1)
rSn = a(r + r2 + r3 + ... + rn)
Kurangi bentuk rSn dengan bentuk Sn untuk mengeleminasi beberapa suku.
rSn-Sn = a(r + r2 + r3 + ... + rn) - a(1 + r + r2 + ... + rn-1)
Sn(r-1) = a(r + r2 + r3 + ... + rn - 1 - r - r2 - ... - rn-1)
Perhatikan bahwa pada bentuk terakhir ini ada suku-suku sejenis yang memiliki tanda berlawanan. Pasangan suku-suku sejenis yang memiliki tanda berlawanan ini hasilnya sama dengan nol. Suku-suku yang masih tersisa adalah rn dan -1, sehingga kita peroleh bentuk berikut ini.
Sn(r-1) = a(rn - 1)
Bentuk terakhir di atas merupakan rumus umum deret geometri yang memiliki suku pertama a dan rasio r dengan r > 1. Sedangkan untuk deret geometri yang memiliki suku pertama dan rasio r yang memiliki batas -1 < r < 1 rumus deret geometrinya adalah sebagai berikut.
Dua jenis rumus di atas diperoleh dengan cara penurunan yang sama, tapi untuk batas rasio yang berbeda. Barisan geometri yang memiliki batas rasio r > 1 disebut sebagai barisan geometri divergen, yaitu barisan geometri dengan suku-suku yang memiliki nilai semakin besar dan tidak menuju ke suatu bilangan. Sedangkan barisan geometri dengan batas rasio -1 < r < 1 disebut sebagai barisan geometri konvergen, yaitu barisan geometri dengan suku-suku yang memiliki nilai semakin mengecil dan menuju ke suatu bilangan.
4. Diketahui : 1/1.2 + 1/2.3 + 1/3.4 +.... + 1/n( n+1 ) = n/n+ 1
JAWAB :
ditanya : buktikkan bahwa setiap bilangan asli
Penyelesaian =
2n-3<2n-2
=2(1)-3<2(1)-2
=(-1)<0(benar)
2(2) -3<2(2) -2
=1<2 (benar)
2(3) -3<2(3) -2
=3<4(benar)
2(4) -3<2(4) -2
=5<6( benar)
2(5) -3<2(5) -2
=7<8( benar)
8. Diketahui : persamaan x+2y=4
Penyelesaian =
gula = x
beras = y
5x + 30y = 410.000 |x 2
2x + 60y = 740.000 |x 1
10x + 60y = 820.000
2x + 60y = 740.000
_________________-
8x = 80.000
x = 10.000
subtitusikan x nya ke persamaan
2x + 60y = 740.000
2(10.000) + 60y = 740.000
20.000 + 60y = 740.000
60y = 720.000
y = 12.000
jadi, harga 1kg gula = Rp 10.000 dan 1kg beras = Rp 12.000
maka 2kg gula dan 5kg beras
= 2(10.000) + 5(12.000)
= 20.000 + 60.000
= Rp 80.000
10. Tentukan daerah bersih pertidaksamaan linear berikut 5x+3y<15
penyelesaian=
Penyelesaian =
13. Ditanya = Daerah yang diarsir pada gambar di bawah adalah himpunan penyelesaian dari sistem pertidaksamaan…
14. Ditanya = Tentukan nilai maksimum dari 3x + 2y yang memenuhi x + y ≤ 5 , x ≥ 0 , y ≥ 0, dan x , y ∈ R.
Penyelesaian =
Penjelasan =
Model || Polos || Garis || Harga
I || 1 || 3 || 150.000
II || 2 || 1 || 100.000
Stok || 20 || 20 || maksimum
(2) Kita buat kalimat matematika dari Tabel diatas Dengan kain polos sebagai (x) dan kain bergaris sebagai (y) :
x + 2y ≤ 20
3x + y ≤ 20
dengan :
x ≥ 0
y ≥ 0
Dan Fungsi Tujuan adalah harga jual :
150.000x + 100.000y
(3) Tentukan nilai fungsi x dan y pada grafik fungsi :
Dari x + 2y = 20 :
x = 0, y ⇒ 0 + 2y = 20
⇒ 2y = 20
⇒ y = 20/2
⇒ y = 10
Titik Koordinat ⇒ (0,10)
y = 0, x ⇒ x + 2y = 20
⇒ x + 0 = 20
⇒ x = 20
Titik Koordinat ⇒(20,0)
Dari 3x + y = 20
x = 0 , y ⇒ 3x + y = 20
⇒ 0 + y = 20
Titik Koordinat ⇒ (0,20)
y = 0, x ⇒ 3x + y = 20
⇒ 3x + 0 = 20
⇒ 3x = 20
⇒ x = 20/3
Titik Koordinat ⇒ (20/3,0)
Dari Titik - titik tersebut tarik garis lurus hingga terhubung.
Lalu kita cari titik potong dari garis tersebut, dengan metode eliminasi dan subtitusi :
Eliminasi y :
x + 2y = 20 | x 1 | x + 2y = 20
3x + y = 20 | x 2 | 6x + 2y = 40
============ -
-5x = -20
x = 20/5
x = 4
Subtitusikan nilai x pada persamaan 3x + y = 20 :
3 . 4 + y = 20
12 + y = 20
y = 20 - 12
y = 8
Koordinat titik potong garis pada (4,8)
(4) Selanjutnya Dari Titik - titik yang berpotongan kita uji dengan :
Fungsi Tujuan f(x,y) = 150.000x + 100.000y :
Ada 3 titik pada Grafik (perhatikan lampiran)
A. Titik (0,10) = 150.000 . (0) + 100.000 . (10) =
= 0 + 1.000.000 = 1.000.000
B. Titik (4,8) = 150.000 . (4) + 100.000 . (8) =
= 600.000 + 800.000 = 1.400.000
C. Titik (20/3,0) = 150.000 . (20/3) + 100.000 . (0) =
= 1.000.000 + 0 = 1.000.000
Dari Hasil Uji diatas dapat dilihat, penghasilan terbesar pada titik (4,8) yaitu sebesar Rp.1.400.000,00
diket:
ditanya:
det C...?
jawab:
- mencari transpos matrisk A
⇒
- mencari matriks C
- mencari det C
det C = (3)(3) - (-6)(8)
= 9 + 48
det C = 57
18. Ditanya = Matriks At adalah transpose matriks A. Jika matriks C = (4/7 -1/7 -1/7 2/7) B = (4 2 2 8) dan A = C-1 maka determinan dari matriks At.B adalah...
Penyelesaian =
Penyelesaian =
Suatu matriks tidak mempunyai invers jika determinan matriks tersebut sama dengan nol
Jadi
|A| = 0
(2x + 1)(5) – 3(6x – 1) = 0
10x + 5 – 18x + 3 = 0
8 – 8x = 0
8 = 8x
x =
x = 1
20. Ditanya = diketahui matriks a= ( 3, y, 5,-1) , b= ( x,5,-3,6), dan c = ( -3,-1, y, 9) . jika a+ b - c = ( 8, 5x, -x , -4) nilai x + 2xy + y adalah..
Penyelesaian =
22. Suatu perusahaan pakaian, JCloth, memiliki dua pabrik yang terletak di Surabaya dan Malang. Di dua pabrik tersebut, JCloth memproduksi dua jenis pakaian, yaitu kaos dan jaket. Perusahaan tersebut memproduksi pakaian yang kualitasnya dapat dibedakan menjadi tiga jenis, yaitu standard, deluxe, dan premium. Tahun kemarin, pabrik di Surabaya dapat memproduksi kaos sebanyak 3.820 kualitas standard, 2.460 kualitas deluxe, dan 1.540 kualitas premium, serta jaket sebanyak 1.960 kualitas standard, 1.240 kualitas deluxe, dan 920 kualitas premium. Sedangkan pabrik yang terletak di Malang dapat memproduksi kaos sebanyak 4.220 kualitas standard, 2.960 kualitas deluxe, dan 1.640 kualitas premium, serta jaket sebanyak 2.960 kualitas standard, 3.240 kualitas deluxe, dan 820 kualitas premium dalam periode yang sama.
Penyelesaian =
Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.
Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.
23. Arman membeli 5 pensil dan 3 penghapus, sedangkan susi membelu 4 pensil dan 2 penghapus di toko yang sama. Di kasir, arman membayar Rp. 11.500 sedangkan susi membayar RP. 9.000. Jika doni membeli 6 dan 5 penghapus, berapa ia harus membayar?
Penyelesaian =
x = pensil
y = penghapus
5x + 3 y = 11.500 (x2)
4x + 2 y = 9.000 (x3)
_______________
10x + 6 y = 23.000
12x + 6y = 27.000
_______________ (-)
-2x = -4.000
x = 2.000
4x + 2y = 9.000
(4x2000) + 2y = 9000
2y = 1000
y = 500
jadi harga pensil = 2000 dan penghapus = 500
sehingga doni harus membayar (6x2000) + (5x500) = 12.000+2.500 = 14.500
24. Bu Ani seorang pengusaha makanan kecil yang menyetorkan dagangannya ke tiga kantin sekolah. Tabel banyaknya makanan yang disetorkan setiap harinya sebagai berikut. Kacang Keripik Permen Kantin A | 10 | 10 | 5 | Kantin B | 20 | 15 | 8 | Kantin C | 15 | 20 | 10 | (Dalam satuan bungkus) Harga sebungkus kacang, sebungkus keripik, dan sebungkus permen berturut-turut adalah Rp 2.000,00; Rp 3.000,00; dan Rp 1.000,00. Hitung pemasukan Bu Ani dari setiap kantin dengan cara perkalian matriks
Perkalian Matriks A dan Matriks B
AB =
AB =
Kantin A: Rp. 55.000,00
Kantin B: Rp. 93.000,00
Kantin C: Rp. 100.000,00
Penyelesaian=
3x + 4y = 55
Jika ditulis dalam bentuk matriks:
Jadi, Lisa bekerja selama 9 jam sedangkan Muri bekerja selama 7 jam.
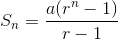
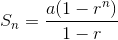
Tidak ada komentar:
Posting Komentar