LOGIKA MATEMATIKA - Dalam logika matematika, kita belajar untuk mementukan nilai dari suatu pernyataan, baik bernilai benar atau salah. Pernyataan sendiri terbagi menjadi 2 jenis, yaitu:
1. Pernyataan tertutup (kalimat tertutup)
Pernyataan tertutup atau kalimat tertutup adalah suatu pernyataan yang sudah memiliki nilai benar atau salah.
Contoh:
“5 adalah bilangan genap”, kalimat tersebut bernilai salah karena yang benar adalah “5 adalah bilangan ganjil”.
2. Pernyataan terbuka (kalimat terbuka)
Pernyataan terbuka atau kalimat terbuka adalah suatu pernyataan yang belum dapat ditentukan nilai kebenarannya karena adanya suatu perubah atau variabel.
Contoh logika matematika:
Saat , maka
bernilai salah
Saat , maka
bernilai benar
3. Ingkaran/negasi/penyangkalan (~)
Dari sebuah pernyataan, kita dapat membuat pernyataan baru berupa “ingkaran/negasi/penyangkalan” atas pernyataan tadi. Berikut adalah tabel kebenaran ingkaran:

*B = pernyataan bernilai benar
S = pernyataan bernilai salah
Artinya, jika suatu pertanyaan (p) benar, maka ingkaran (q) akan bernilai salah. Begitu pula sebaliknya. Berikut adalah contoh dalam matematika:
- p: Besi memuai jika dipanaskan (pernyataan bernilai benar)
- ~p: Besi tidak memuai jika dipanaskan (pernyataan bernilai salah).
Contoh lain:
- p: Semua unggas adalah burung.
- ~p: Ada unggas yang bukan burung.
4. Konjungsi (∧)
Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘dan’ sehingga membentuk pernyataan majemuk ‘p dan q’ yang disebut konjungsi yang dilambangkan dengan “p∧q”. Berikut adalah tabel kebenaran konjungsi.
| p | q | p∧q |
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | S |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep konjungsi akan bernilai benar jika dan hanya jika kedua pernyataan (p dan q) benar
Contoh:
Budi sudah makan belajar dan makan
Misalkan, untuk dapat diizinkan bermain oleh Ibu, Budi harus memenuhi kondisi di atas. Jika satu saja atau bahkan kedua pernyataan tersebut dilanggar, maka Budi tidak diizinkan untuk bermain.
5. Disjungsi
Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘atau’ sehingga membentuk pernyataan majemuk ‘p atau q’ yang disebut disjungsi yang dilambangkan dengan “p ∨ q”. Berikut adalah tabel kebenaran disjungsi.
| p | q | p∨q |
| B | B | B |
| B | S | B |
| S | B | B |
| S | S | S |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep disjungsi hanya akan bernilai salah jika kedua pernyataan (p dan q) salah.
Contoh:
Bandung atau Palembang adalah kota yang terletak di Pulau Jawa
Pernyataan Bandung adalah kota yang terletak di Pulau Jawa adalah benar. Pernyataan Palembang adalah kota yang terletak di Pulau Jawa adalah salah. Sehingga pernyataan Bandung atau Palembang adalah kota yang terletak di Pulau Jawa bernilai benar.
6. Implikasi (⟹)
Implikasi bisa dipandang sebagai hubungan antara dua pernyataan di mana pernyataan kedua merupakan konsekuensi logis dari pernyataan pertama. Implikasi ditandai dengan notasi ‘⟹’. Misalkan p, q adalah pernyataan, implikasi berikut
p ⟹ q
dibaca ‘jika p maka q’. Berikut adalah tabel kebenaran disjungsi.
| p | q | p⇒q |
| B | B | B |
| B | S | S |
| S | B | B |
| S | S | B |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep implikasi akan bernilai salah jika dan hanya jika sebab bernilai benar namun akibat bernilai salah. Selain itu implikasi bernilai benar.
Contoh:
Jika Budi sembuh maka Budi akan sekolah
Jika betul Budi sembuh lalu Budi masuk sekolah, Budi telah melakukan hal yang benar. Namun jika Budi sembuh namun dia tidak masuk sekolah, Budi telah berbuat salah karena mengingkari janjinya. Lalu, bagaimana jika Budi belum sembuh? Perhatikan bahwa Budi hanya berjanji masuk sekolah jika dia sembuh. Akibatnya jika dia masih belum sembuh, tidak masalah bagi Budi untuk masuk sekolah ataupun tidak karena dia tidak melanggar janjinya.
7. Biimplikasi
Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘jika dan hanya jika’ sehingga membentuk pernyataan majemuk ‘p jika dan hanya jika q’ yang disebut biimplikasi yang dilambangkan dengan “p ⇔ q”. Berikut adalah tabel kebenaran biimplikasi:
| p | q | p⇔q |
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | B |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep biimplikasi akan bernilai benar jika sebab dan akibatnya (pernyataan p dan q) bernilai sama. Baik itu sama-sama benar, atau sama-sama salah.
Contoh:
Ayah mendapatkan gaji jika dan hanya jika ayah bekerja
Jika ayah mendapatkan gaji maka ayah bekerja dan jika ayah telah bekerja maka ayah akan mendapat gaji. Sebalinya, jika ayah tidak mendapatkan gaji maka ayah sedang tidak bekerja dan jika ayah tidak bekerja maka ayah tidak akan mendapat gaji.
8. Ekuivalensi pernyataan majemuk
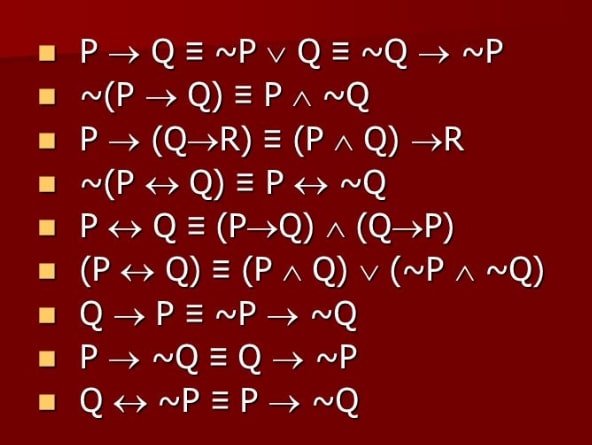

Tidak ada komentar:
Posting Komentar