PENGERTIAN TURUNAN DAN SIFAT-SIFATNYA BERSAMA CONTOH SOALNYA

 

Thrilia Rachianingrum 

(35) XI IPS 2

PENGERTIAN TURUNAN DAN 

SIFAT-SIFATNYA 

    

Definisi Turunan

    Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel).

    Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.

Menggunakan konsep limit yang sudah dipelajari, turunan dapat didefinisikan sebagai

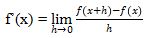
turunan tersebut didefinisikan sebagai limit dari perubahan rata-rata dari nilai fungsi terhadap variabel x.

Selanjutnya akan dijelaskan mengenai contoh penerapan turunan.

Penerapan Turunan

Berikut merupakan beberapa penerapan turunan.

• Turunan dapat diterapkan untuk menghitung gradien dari garis singgung suatu kurva.
• Turunan dapat digunakan untuk menentukan interval dimana suatu fungsi naik atau turun.
• Turunan dapat diterapkan untuk menentukan nilai stasioner suatu fungsi.
• Turunan dapat diterapkan dalam menyelesaikan permasalahan yang berkaitan dengan persamaaan gerak.
• Turunan dapat digunakan untuk menyelesaikan permasalahan maksimum-minimum.

Berikut ini akan dijelaskan mengena rumus turunan.

Rumus Turunan

Berikut merupakan beberapa rumus dasar untuk menentukan turunan.

• f(x) = c, dengan c merupakan konstanta

Turunan dari fungsi tersebut adalah f’(x) = 0.

• f(x) = x

Turunan dari fungsi tersebut adalah f’(x) = 1.

• f(x) = axn

Turunan dari fungsi tersebut adalah f’(x) = anxn – 1

• Penjumlahan fungsi:  h(x) = f(x) + g(x)

Turunan fungsi tersebut yaitu h’(x) = f’(x) + g’(x).

• Pengurangan fungsi: h(x) = f(x) – g(x)

Turunan fungsi tersebut adalah h’(x) = f’(x) – g’(x)

• Perkalian konstanta dengan suatu fungsi (kf)(x).

Turunan fungsi tersebut adalah k . f’(x).

Sifat-sifat Turunan

1. Jika $f(x)=c$ dimana $c$ adalah konstanta, maka turunannya adalah$f'(x)=0$

Contoh:$\begin{aligned} f(x)&=2 &\rightarrow f'(x)=0\\ f(x)&=13 &\rightarrow f'(x)=0\\ f(x)&=100 &\rightarrow f'(x)=0 \end{aligned}$

2. Jika $f(x)=cx$, maka turunannya adalah$f'(x)=c$

Contoh:$\begin{aligned} f(x)&=2x &\rightarrow &f'(x)=2\\ f(x)&=13x &\rightarrow &f'(x)=13\\ f(x)&=100x &\rightarrow &f'(x)=100 \end{aligned}$

3. Jika $f(x)=x^n$ maka turunannya adalah$f'(x)=nx^{n-1}$

Contoh:$\begin{aligned} f(x)&=x^4 &\rightarrow &f'(x)=4x^3\\ f(x)&=x^3 &\rightarrow &f'(x)=3x^2\\ f(x)&=x^2 &\rightarrow &f'(x)=2x \end{aligned}$

4. Jika $f(x)=cx^n$maka turunannya adalah$f'(x)=cnx^{n-1}$

Contoh:$\begin{aligned} f(x)&=2x^4 &\rightarrow &f'(x)=8x^3\\ f(x)&=13x^3 &\rightarrow &f'(x)=39x^2\\ f(x)&=100x^2 &\rightarrow &f'(x)=200x \end{aligned}$

5. Jika $f(x)=c\,u(x)$ maka turunannya adalah$f'(x)=c\,u'(x)$

Contoh:$\begin{aligned} f(x)&=4\ln{x}&\rightarrow &f'(x)=4\frac{1}{x}\\ f(x)&=3\cos{x}&\rightarrow &f'(x)=3\sin{x}\\ f(x)&=2\sin{x}&\rightarrow &f'(x)=-2\cos{x} \end{aligned}$

6. Jika $f(x)=u(x)\pm v(x)$ maka turunannya adalah$f'(x)=u'(x)\pm v'(x)$

Contoh:$\begin{aligned} f(x)&=2x+x^2&\rightarrow &f'(x)=2+2x\\ f(x)&=x^4-x^3&\rightarrow &f'(x)=4x^3-3x^2\\ f(x)&=\sin{x}+\cos{x}&\rightarrow &f'(x)=\cos{x}-\sin{x} \end{aligned}$

7. Jika $f(x)=u(x)v(x)$ maka turunannya adalah$f'(x)=u'(x)v(x)+u(x)v'(x)$

Contoh:$f(x)=x^4x^3$Misalkan $u(x)=x^4$ dan $v(x)=x^3,$ maka $u'(x)=4x^3$ dan $v'(x)=3x^2,$ sehingga$\begin{aligned} f'(x)&=(4x^3)(x^3)+(x^4)(3x^2)\\ &=4x^6+3x^6\\ &=7x^6 \end{aligned}$

8. Jika $f(x)=\displaystyle\frac{u(x)}{v(x)}$ maka turunannya adalah$f'(x)=\frac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2}$

Contoh:$f(x)=\frac{x^4}{x^3}$Misalkan $u(x)=x^4$ dan $v(x)=x^3,$ maka $u'(x)=4x^3$ dan $v'(x)=3x^2,$ sehingga$\begin{aligned} f'(x)&=\frac{(4x^3)(x^3)-(x^4)(3x^2)}{(x^3)^2}\\ &=\frac{4x^6-3x^6}{x^6}\\ &=1 \end{aligned}$

9. Jika $f(x)={u(x)}^n$ maka turunannya adalah$f'(x)=n(u(x))^{n-1}u'(x)$

Contoh:$f(x)=(2x+x^2)^4$Misalkan $u(x)=2x+x^2,$ sehingga $u'(x)=2+2x,$ maka$f'(x)=4\left(2x+x^2\right)^3(2+2x)$

Contoh Soal Turunan

1. Tentukan turunan dari fungsi berikut.

• f(x) = 8
• g(x) = 3x + 5
• h(x) = 6x3
• k(x) = 3x5/3
• m(x) = (3x2 + 3)4

Pembahasan

• f’(x) = 0
• g’(x) = 3
• h’(x) = 6 (3) x3 – 1 = 18x2
• k’(x) = 3 (5/3) x(5/3) – 1 = 5x2/3
• m’(x) = 4 . (3x2 + 3)4 – 1 . 6x = 24x . (3x2 + 3)3

2. Tentukan turunan dari fungsi berikut.

f(x) = (3x + 2) . (2x2 – 1)

Pembahasan

Misal: u(x) = 3x + 2 dan v(x) = 2x2 – 1

f’(x) = u’(x) . v(x) + u(x) . v’(x)

f’(x) = 3 . (2x2 – 1) + (3x + 2) . (4x)

f’(x) = 6x2 – 3 + 12x2 + 8x = 18x2 + 8x – 3

3. Diberikan sebuah fungsi ordo 2 seperti di bawah ini

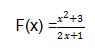
Tentukan nilai f(0) + 3f’(1)

Pembahasan

Untuk mengerjakan soal ini, kita dapat memasukkan nilai 0 ke dalam fungsi tersebut.

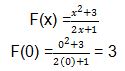
Setelah Anda, mendapatkan nilai f(0). Kita dapat mengerjakan turunan fungsi hasil bagi menggunakan salah sifat turunan.

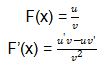
Untuk menggunakan rumus tersebut, kita dapat menggunakan pemisalan dan turunannya seperti di bawah ini.

U = x2 + 3 ; U’ = 2x

V = 2x + 1 ; V’ = 2

Kemudian, kita bisa memasukkan pemisalan tersebut ke dalam rumus turunan yang sebelumnya serta kita dapat secara langsung memasukkan f’x(1).

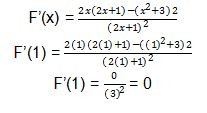
Maka, hasil f(0) + 3f’(1) = 3 + 3(0) = 3

4. Tentukan hasil turunan f(x) = (x2 + 2x + 3)(3x + 2)

Pembahasan

Sama seperti soal sebelumnya, Untuk mengerjakan soal turunan dalam bentuk perkalian, kita dapat menggunakan rumus sifat turunan serta menggunakan pemisalan dalam fungsi tersebut seperti di bawah ini.

F’(x) = u’v + uv’

U = x2 + 2x + 3 ; U’ = 2x + 3

V = 3x + 2 ; V’ = 3

F’(x) = u’v + uv’

F’(x) = (2x+3)(3x + 2) + (x2 + 2x + 3)(3)

F’(x) = 6x2 + 13x + 6 + 3x2 + 6x + 9

F’(x) = 9x2 + 19x + 15

Sehingga bentuk akhir F’(x) adalah 9x2 + 19x + 15

5. Jika terdapat f(x) = (2x-1)2(x+2). Berapakah nilai f’x(2)

Pembahasan

Untuk mengerjakan soal ini, kita bisa menggunakan sifat turunan fungsi f’(x) = u’v + v’u untuk mendapatkan hasil akhir. Sehingga kita dapat melakukan pemisalan kembali.

F’(x) = u’v + uv’

U= (2x-1)2 = 4x2 – 4x + 1 ; U’ = 8x – 4

V = x + 2 ; V’ = 1

F’(x) = u’v + uv’

F’(x) = (8x – 4)(x + 2) + (4x2 – 4x + 1)(1) ; kita dapat memasukkan nilai 2 seperti di soal

F’(2) = ((8(2) – 4)(2 + 2)) + ((4(2)2 – 4(2) + 1)(1))

F’(2) = ((16-4)(4)) + ((16-8+1)(1))

F’(2) = 96 + 9 = 105

Sehingga nilai akhir F’(2) adalah 105

6. Tentukan sebuah garis singgung pada kurva y= -2x2 + 6x + 7 yang tegak lurus dengan garis x – 2y +13 = 0

Pembahasan

Disebutkan di dalam soal bahwa terdapat 2 garis yang saling tegak lurus, sehingga kita dapat mengasumsikan bahwa kedua garis memiliki kemiringan tertentu. Kita dapat menentukan nilai m1 dan m2 dari kedua garis.

m1 merupakan slope dari garis y= -2x2 + 6x + 7. Untuk mencari nilai m1, dapat dilakukan dengan cara menurunkan fungsi y= -2x2 + 6x + 7.

m1 = y’(x) = -4x + 6

m2 merupakan slope dari x – 2y +13. Untuk mencari nilai m2, kita harus mengubah fungsi tersebut menjadi fungsi y.

x – 2y +13 = 0

x + 13 = 2y

y = 0,5x + 6.5

m2 = y’(x) = 0,5

Dikarenakan kedua garis saling tegak lurus, maka nilai m1 x m2 = -1.

m1 x m2 = -1

(-4x + 6)0,5 = -1

-2x + 3 = -1

-2x =  -4

X = 2

Kita masukkan ke dalam persamaan m1 sehingga di dapatkan nilai m1 = -2. Setelah menemukan nilai x, kita masukkan nilai tersebut ke fungsi y sehingga di dapatkan nilai y = 11.

Untuk membuat sebuah garis singgung, rumus yang digunakan adalah (y-y1) = m1(x – x1).

(y – 11) = -2 (x – 2)

Y – 11 = -2x +4

Y = -2x + 15

Garis singgung adalah y+2x-15 = 0

7. Terdapat sebuah box tanpa tutup dengan alas berbentuk persegi memiliki luas sebesar 512 cm2. Berapakah panjang rusuk agar volumenya memiliki nilai maksimum

Pembahasan

Pada soal tersebut, dijelaskan bahwa box tidak memiliki tutup. Sehingga, box tersebut terdiri dari 4 sisi dan 1 alas. Anggap sisi alas adalah s dan tinggi sisi adalah t. Kita dapat menuliskan persamaan box seperti di bawah ini.

512 = luas alas + 4 sisi box

512 = s.s + 4.s.t
512 = s2 + 4st
512 – s2 = 4st

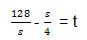
Setelah mendapatkan t, kita bisa mencari volume dari box tersebut

V = s3 = s2 . t

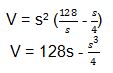
Untuk mendapatkan volume maksimum, kita dapat menurunkan persamaan volume di atas

V’(s) = 0

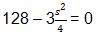
S2 = 170,67 cm2

S = 13,07 cm

Sehingga, panjang s yang dibutuhkan agar volumenya maksimum adalah 13,07 cm.

DAFTAR PUSTAKA

https://www.rumusstatistik.com/2018/07/sifat-sifat-turunan.html