FUNGSI LINEAR
Fungsi linear merupakan seuah fungsi y = f(x) dengan f(x) = ax + b (a, b ∈ R dan a ≠ 0) untuk seluruh x dalam daerah asalnya.
Fungsi linear juga dikenal sebagai fungsi polinom (sukubanyak) berderajat satu dalam variable x.
Fungsi linear sendiri memiliki bentuk umum sebagai berikut:
f : x → mx + c atau
f(x) = mx + c atau
y = mx + c
m merupakan gradien atau kemiringan atau kecondongan dan c merupakan konstanta
Melukis Grafik Fungsi Linier
Berikut ini adalah beberapa langkah untuk melukis grafik fungsi linier, antara lain:
- Menentukan titik potong dengan sumbu x, y = 0 didapatkan koordinat A( x1, 0)
- Menentukan titik potong dengan sumbu y, x = 0 didapatkan koordinat B( 0, y1)
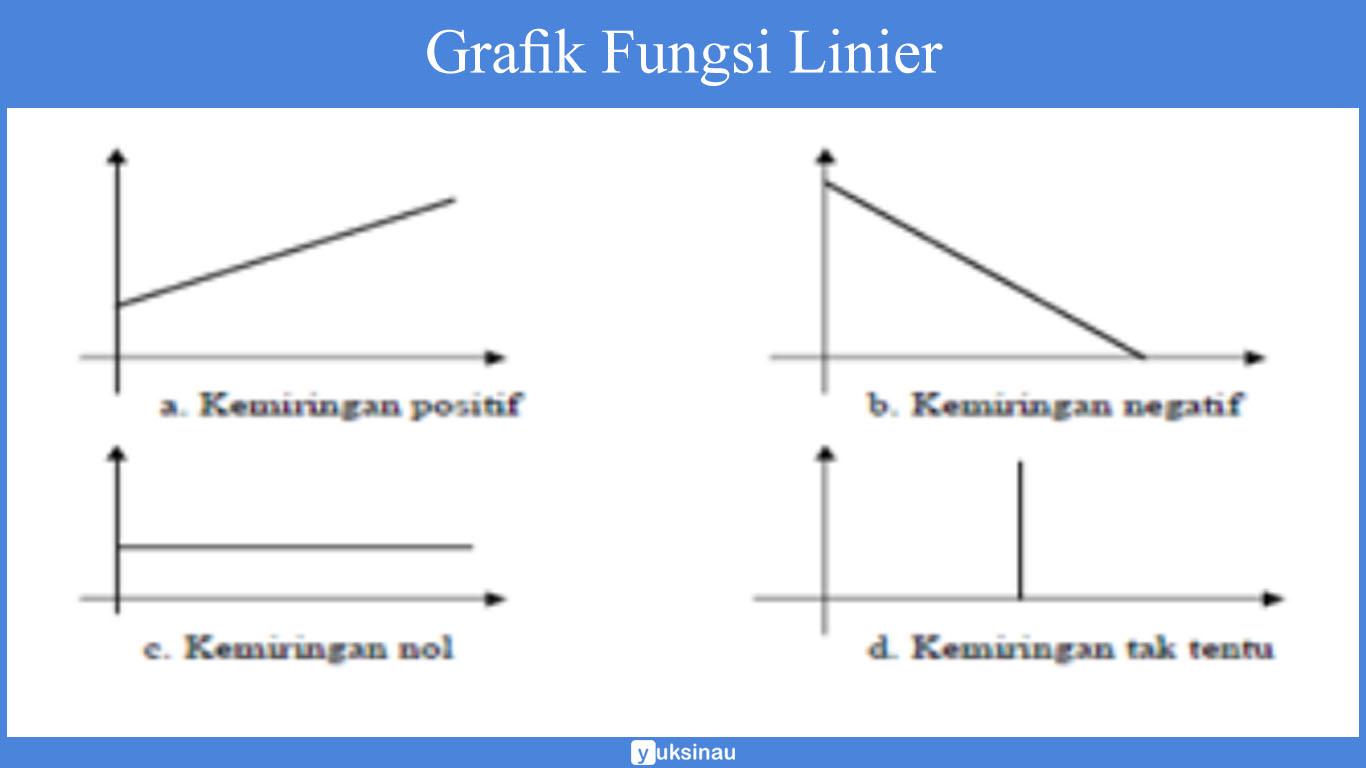
- Menghubungkan dua titik A dan B sehingga akan terbentuk garis lurus Persamaan linier yang bisa juga ditulis ditulis dengan menggunakan simbol y = ax + b. (Hal ini untuk memudahkan kita dalam memahami gambar). Apabila b bernilai positif maka fungsi linier akan dilukis garis dari kiri bawah ke kanan atas
- Apabila b bernilai negatif maka fungsi linier akan digambarkan garis dari kiri atas ke kanan bawah.
- Apabila b bernilai nol maka fungsi linier akan digambarkan garis yg sejajar dengan sumbu datar x.
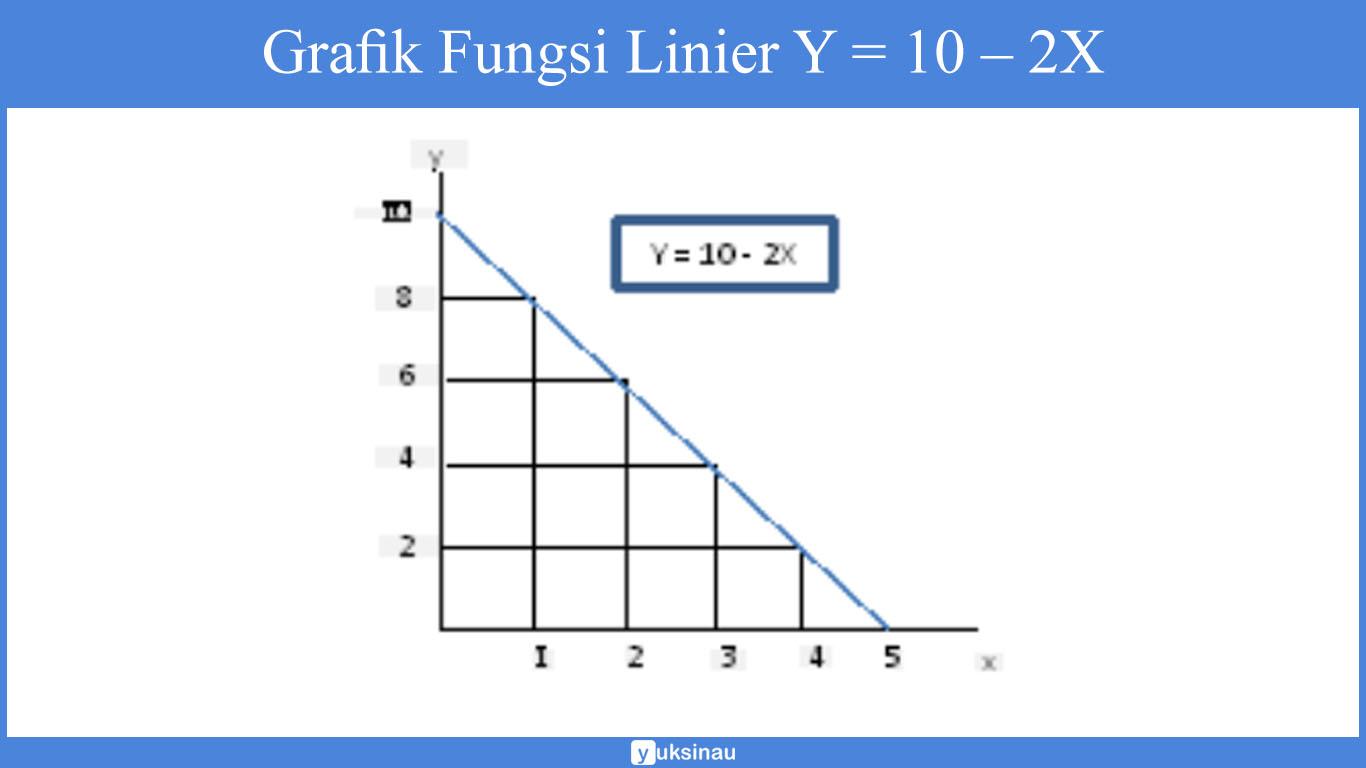
Jika b bernilai negatif, disini kita contohkan dengan Y = 10 – 2X maka kurva akan bergerak dari kiri atas ke kanan bawah, berikut gambarnya:
Jika b bernilai positif : Y = 2 + 2X maka kurva akan bergerak dari arah kiri bawah ke kanan atas, beirkut ini adalah gambarnya:
Gradien dan Persamaan Garis Lurus Fungsi linear
a. Garis lurus yang melewati titik A(x1, y1) dan B(x2, y2) mempunyai gradien m:
m = y1-y2 atau m = y2-y1
x1-x2 x2-x1
b. Persamaan garis lurus yang melewati titik A(x1, y1) dan B(x2, y2) yaitu:
y-y1 = x-x1
y2-y1 x2-x1
c. Persamaan garis lurus (pgl) yang bergradien m serta melewati titik A(x1, y1) yaitu:
y = m (x – x1 ) + y1
Menentukan Gradien dari Persamaan Garis Lurus (pgl)
Berikut adalah cara untuk menentukan gradien dari persamaan garis lurus (pgl)
- Persamaan garis lurus: ax + by = c, sehingga gradiennya m = – a/b
- Persamaan garis lurus: y = ax + b, sehingga m = a
- Garis yang sejajar sumbu x mempunyai persamaan y = c dan juga m = 0
- Garis yang sejajar sumbu y mempunyai persamaan x = c serta tidak mempunyai gradient
Titik potong dua buah garis
Menentukan titik potong dari dua buah garis lurus identik dengan menyelesaikan permasalah dari sistem persamaan linier dua variabel. Baik itu dengan menggunakan metode eleminiasi, metode substitusi ataupun metode grafik.
Hubungan dua buah garis
Dua garis yang bergradien m1 dan m2 akan disebut sejajar apabila m1 = m2 dan tegak lurus apabila m1 x m2 = -1.
Berimpit
Dua garis lurus akan berimpit apabila persamaan garis yang satu merupakan kelipatan dari garis yang lain. Dengan demikian , garis 
akan berimpit dengan garis 
, apabila 
Sejajar
Dua garis lurus akan sejajar jika lereng atau gradien garis yang satu sama dengan lereng atau gradien dari garis yang lain.
Dengan begitu, garis 
akan sejajar dengan garis 
, apabila 
.
Berpotongan
Dua garis lurus akan berpotongan jika lereng atau gradien garis yang satu tidak sama dengan lereng atau gradien dari garis yang lain. Dengan begitu, garis akan berpotongan dengan garis , apabila 
.
Tegak lurus
Dua garis lurus akan saling tegak lurus jika lereng atau gradien garis yang satu adalah kebalikan dari lereng atau gradien dari garis yang lain dengan tanda yang berlawanan. Dengan begitu, garis 
akan tegak lurus dengan garis 
, apabila atau 
.
Persamaan Kuadrat Fungsi linear
Persamaan kuadrat adalah bentuk persamaan di mana pangkat terbesar variabelnya yaitu 2.
Bentuk umum dari persamaan kuadrat ialah sebagai berikut: y = ax2 + bx + c = 0 dengan a ≠ 0, a, b, dan c merupakan koefisien. Serta x adalah variabelnya.
Sebagai contoh: x2 + 5x + 6, 2x2 – 3x + 4, dan lain sebagainya.
Menentukan Akar-akar Persamaan Kuadrat
Akar-akar persamaan kuadrat dalam hal ini maksudnya yaitu nilai x yang membuat ax2 + bx + c hasilnya akan sama dengan 0.
Sebagai contohnya, apabila x= k membuat ak2 + bk + c = 0, maka k akan disebut seabgai akar-akar dari persamaan kuadrat ax2 + bx + c = 0.
Untuk menentukan akar-akar, terdapat tiga metode yang dapat kalian pakai.
Antara lain: metode pemfaktoran, melengkapkan kuadrat sempurna, serta metode rumus abc.
Tetapi metode melengkapkan kuadrat sempurna jarang atau cukup sulit untuk dipakai dalam menentukan akar-akar, sehingga kita tidak akan membahasnya pada artikel ini.
Metode Pemfaktoran
Persamaan kuadrat ax2 + bx + c = 0 diubah menjadi a(x – x1) (x – x2 ) = 0, sehingga akar-akarnya yaitu x1 dan x2 .
Contohnya, apabila kita ingin memfaktorkan ax2 + bx + c = 0, langkah pertama yang dilakukan adalah mencari dua bilangan. Dalam kasus ini akan kita ambil p dan q.
Sehingga, apabila kita jumlahkan akan memperoleh hasil b. Sementara apabila kita kalikan akan menghasilkan ac.
Dengan kata lain, p + q = b dan p . q = a .c
Apabila a = 1, maka bentuk pemfaktorannya yaitu ( x + p )( x + q ) = 0, sehingga akar-akarnya yaitu x + p = 0 ⟺ x = -p atau x + q = 0 ⟺ x = -q
Apabila a ≠ 1, maka bentuk pemfaktorannya yaitu 
sehingga akar-akarnya yaitu 
atau 
Sebagai contoh:
Tentukanlah akar-akar dari persamaan kuadrat (a) x2 – 5x + 6 = 0 dan (b) 6x2 – x – 15 = 0
Jawab:
(a)
a = 1, b = -5 dan c = 6. Carilah dua bilangan, p dan q, sehingga p + q = -5 dan p.q = 6.
Kedua bilangan tersebut ialah p = -3 dan q = -2, sebab -3 + (-2) = -5 dan -3 . -2 = 6
Maka pemfaktorannya ialah (x + (-3))(x + (-2)) = 0 atau (x – 3)(x – 2) = 0, sehingga akar-akarnya yaitu:
x – 3 = 0 ⟺ x1 = 3 atau x – 2 = 0 ⟺ x2 = 2
(b)
Sama halnya dengan yang ada pada (a), cari p dan q, sehingga p + q = -1 dan p.q = a.c = -90
Maka akan diperoleh p = -10 dan q = 9
Maka pemfaktorannya yaitu 
, sehingga akar-akarnya ialah 
atau 
Sehingga, akar-akar persamaan kuadrat tersebut yaitu 
atau 
Fungsi Kuadrat
Fungsi kuadrat adalah sebuah fungsi yang pangkat terbesar variabelnya adalah 2.
Sama dengan persamaan kuadrat, tetapi berbentuk sebuah fungsi.
Bentuk umumnya yaitu: f(x) = ax2 – bx + c, dengan a, b, c sebuah bilangan real dan a ≠ 0.
Sebagai contoh: f(x) = 3x2 – 5x + 7
Dengan begitu, f(0) = 3 . 02 + 5 . 0 + 7 = 7, f(0) = 3 . 42 + 5 . 4 + 7 = 75, dan yang lainnya.
Grafik atau Kurva Fungsi Kuadrat
Apabila digambarkan pada koordinat Cartesius, grafik fungsi kuadrat berbentuk parabola.
Parabola nya terbuka ke atas apabila a > 0 dan terbuka apabila a < 0.
Berikut adalah tahapan untuk menggambarkan grafik atau kurva nya:
Langkah pertama menentukan titik potong y = f(x) = ax2 – bx + c terhadap sumbu x. Yakni nila x saat y = 0.
Dengan begitu, nilai titik potong ini adalah akar-akar dari persamaan kuadrat ax2 + bx + c = 0
Selanjutnya, menentukan titik potong terhadap sumbu y, nilai y saat x = 0.
Sesudah itu, menentukan sumbu simetri nya. Sumbu simetri adalah garis yang membagi dua parabola menjadi sama besar. Titik potong sumbu simetri terhadap sumbu x bisa dihitung dengan menggunakan rumus 
atau 
Terakhir, menentukan titik puncak (titik balik maksimum atau minimum) grafiknya. Titik puncak adalah titik di mana nilai y = f(x) mencapai nilai maksimum atau minimum, sehingga parabola nya akan berbalik arah.
Koordinat titik puncak parabola yaitu:
Di mana D merupakan diskriminan, yaitu D = b2 – 4ac.
Setelah memperoleh titik-titik di atas, maka kita bisa langsung menggambar grafik fungsi kuadrat dengan cara menghubungkan titik-titik di atas dengan garis yang berbentuk parabola.
Supaya parabolanya terlihat lebih halus (smooth), kita bisa menghitung atau menentukan titik-titik lain yang dilewati oleh kurva atau fungsi y = f(x).
Berikut adalah contoh dari grafik fungsi kuadrat y = f(x) = x2 – 5x + 4.
Contoh soal:
Apabila y = f(x) = 2x2 – 11x + p memiliki nilai minimum -1/8, maka tentukanlah nilai p.
Jawab:
Nilai minimum tersebut adalah titik puncak dari y = f(x)
Dengan begitu, dengan memakai rumus titik puncak kita bisa peroleh:
Titik puncak = 
Dengan begitu, 
Hubungan Diskriminan Grafik Fungsi Kuadrat
Apabila pada persamaan kuadrat nilai diskriminan bisa kita pakai untuk mengetahui apakah akar-akarnya riil, kembar, atau tidak memiliki akar-akar riil.
Maka pada fungsi kuadrat kita bisa memakai nilai diskriminan untuk mengetahui apakah grafiknya memotong sumbu x di dua titik yang berlainan, menyinggung sumbu x, atau tidak menyinggung maupun memotong sumbu x.
Berikut ini adalah sifat-sifatnya:
Apabila D adalah diskriminan suatu fungsi kuadrat f(x) = ax2 – bx + c, maka
Apabila D > 0, maka grafik dari y = f(x) akan memotong sumbu x pada dua titik yang berbeda.
Apabila D = o, maka grafik dari y = f(x) akan menyinggung sumbu x pada satu titik.
Apabila D < 0, maka grafik dari y = f(x) tidak akan memotong sumbu 
.
Fungsi Rasional
Fungsi rasional merupakan fungsi yang mempunyai bentuk umum
Adapun fungsi rasional yang paling sederhana, yakni fungsi y = 1/x dan fungsi y = 1/x².
Di mana keduanya mempunyai pembilang konstanta sertaa penyebut polinomial dengan satu suku. Dan kedua fungsi tersebut mempunyai domain semua bilangan real kecuali x ≠ 0.
Fungsi y = 1/x
Fungsi ini disebut juga sebagai fungsi kebalikan sebab setiap kita mengambil sembarang x (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut.
Yang artinya x yang besar akan menghasilkan nilai fungsi yang kecil, begitu juga sebaliknya. Tabel dan grafik dari fungsi tersebut bisa dilihat pada gambar di bawah ini.
Tabel dan grafik di atas menunjukan beberapa hal yang menarik.
Yang pertama, grafik tersebut lolos pada uji garis vertikal. Yang berarti setiap garis vertikal pada bidang koordinat Cartesius akan memotong grafik pada maksimal satu titik.
Sehingga, y = 1/x adalah sebuah fungsi.
Yang kedua, sebab pembagian tidak terdefinisi jadi saat pembaginya nol, maka nol tidak akan mempunyai pasangan, sehingga menghasilkan jeda pada x = 0.
Hal tersebut sesuai dengan domain dari fungsi tersebut, yakni seluruh x anggota bilangan real kecuali 0.
Yang ketiga, fungsi tersebut adalah fungsi ganjil, dengan salah satu cabangnya terletak di kuadran I.
Sementara yang lainnya berada pada kuadran III.
Kemudian yang terakhir, pada kuadran I, saat x menuju tak hingga, nilai y menuju dan mendekati nilai nol.
Secara simbolis bisa kit tuliskan sebagai x → ∞, y → 0. Secara grafis, kurva dari grafik fungsi tersebut akan mendekati sumbu-x pada saat x mendekati tak hingga.
Tak hanya itu saja, kita juga bisa mengamati bahwa pada saat x mendekati nol dari kanan maka nilai y akan mendekati bilangan real positif yang sangat besar (positif tak hingga): x → 0+, y → ∞.
Untuk catatan, tanda + atau – yang berada di atas akan mengindikasikan arah dari pendekatan. Yakni dari sisi positif (+) atau dari sisi negatif (–).
Contoh
Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional
Untuk y = 1/x dalam kuadran III,
- Mendeskripsikan sifat dari ujung grafik fungsi tersebut.
- Mendeskripsikan apa yang akan terjadi pada saat x mendekati nol.
Pembahasan Serupa dengan sifat grafiknya pada kuadran I, maka akan kita peroleh
- Pada saat x mendekati negatif tak hingga, nilai y akan mendekati nol. Jika disimbolkan akan menjadi: x → –∞, y → 0.
- Pada saat x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga bisa kita tuliskan dengan simbol x → 0–, y → –∞.
Fungsi y = 1/x²
Dari pembahasan di atas, kita bisa mengetahui bahwa grafik dari fungsi ini akan mengalami jeda pada saat x = 0.
Namun demikian, sebab kuadrat dari sembarang bilangan negatif merupakan bilangan positif, cabang-cabang dari grafik fungsi ini akan terletak kdi atas sumbu-x.
Perhatikan bahwa fungsi y = 1/x² adalah fungsi genap.
Sama halnya dengan y = 1/x, nilai x yang mendekati positif tak hingga akan menghasilkan y yang mendekati nol. Jika kita tulis simbolnya maka akan menjadi: x → ∞, y → 0.
Hal ini adalah salah satu indikasi dari sifat asimtot dalam arah horizontal. Serta kita akan menyatakan y = 0 adalah asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,
Pada gambar (a) di bawah ini menggambarkan garis asimtot horizontal pada y = 1, yang menunjukan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan.
Gambar (b) menggambarkan garis asimtot horizontal pada y = –2, yang menunjukan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.
